Análisis de métodos iterativos de resolución de sistemas no lineales a partir de la dinámica
Las ecuaciones y los sistemas de ecuaciones no lineales están presentes en diferentes ámbitos de la ciencia y la ingeniería. Este tipo de problemas no tienen una solución analítica conocida, de modo que es necesario recurrir a técnicas numéricas para obtener una solución aproximada.
Las técnicas numéricas para resolver ecuaciones y sistemas no lineales son los métodos iterativos. Existen numerosas clasificaciones acerca de este tipo de esquemas: de un punto o multipunto (Newton vs King), con o sin memoria (Secante vs Newton), óptimos o no óptimos (Newton vs Traub), con o sin derivadas (Newton vs Steffensen), … En función de qué tipo de problema queramos resolver optaremos por un método u otro.
Una característica fundamental de un método iterativo es su orden de convergencia. Nos da una idea de la velocidad con la que se aproxima a la solución. Sin embargo, métodos con altos órdenes de convergencia también requieren de un coste computacional considerable.
Existen tres tipos de convergencia que se utilizan de forma general. La convergencia local implica que existe un conjunto de estimaciones iniciales próximas a la solución que convergen a dicha solución. La convergencia semilocal indica que para un conjunto de estimaciones iniciales se puede garantizar la convergencia a la solución. Por último, la convergencia global asegura que para un conjunto grande de estimaciones iniciales se converge a la solución esperada.
La evaluación de si un método es bueno o no se da a partir del análisis de su estabilidad. En pocas palabras, se dice que un método es estable si para cualquier estimación inicial se consigue alcanzar la solución esperada. Sin embargo, si no se alcanza dicha solución, hay que analizar cuál es el motivo. Estas justificaciones se pueden desarrollar tomando conceptos de dinámica, fundamentados en los documentos de P. Blanchard o R. L. Devaney, entre otros.
El auge de los métodos iterativos está estrechamente ligado al desarrollo computacional. A principios del siglo XXI se aplicaron conceptos de dinámica compleja para analizar los métodos iterativos de resolución de ecuaciones no lineales sobre un conjunto de valores iniciales de variable compleja. De forma paralela, se desarrollaron los conceptos de dinámica real, de modo que las estimaciones iniciales y los valores que resultaban de la aplicación de los métodos debían ser de variable real.
Existen multitud de herramientas gráficas que nos permiten comprobar de un vistazo la estabilidad de un método iterativo y comprobar los motivos por los cuales es posible que para determinadas estimaciones iniciales el método no converja a la solución esperada. La herramienta principal es el plano dinámico, cuyas implementaciones en Mathematica y Matlab fueron publicadas por J. L. Varona y F. I. Chicharro, respectivamente. El plano dinámico asigna un color a cada una de las soluciones de una ecuación no lineal. Estas soluciones también se conocen como puntos fijos atractores, pero es posible que haya más puntos fijos atractores diferentes de las soluciones, lo que empeoraría la calidad del método iterativo. Se selecciona un conjunto de números complejos como estimaciones iniciales y se aplica el método iterativo a cada una de ellas. Si el punto converge a una de las soluciones, se representa con el color correspondiente a dicha solución; en caso contrario, se representa en color negro. Además, la intensidad del color se gradúa en función de las iteraciones que ha tardado en convergen, de modo que puntos El conjunto de todas las estimaciones iniciales que convergen a una solución se denomina cuenca de atracción de dicho punto fijo atractor.
Veamos un par de ejemplos de planos dinámicos relacionados con el método de Newton. Este método tiene la expresión iterativa
De modo que, dada una estimación inicial se obtienen los diferentes iterados hasta un determinado criterio de parada. Este criterio puede estar basado en la diferencia entre los dos últimos iterados, la diferencia del iterado actual con la solución si es conocida, el valor de la función en el último iterado, u otras combinaciones posibles.
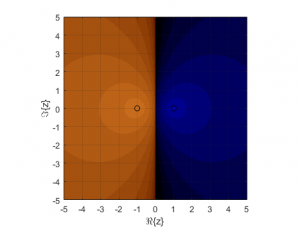
Cuando aplicamos el método de Newton sobre la ecuación no lineal 
, sabemos de antemano que las soluciones van a ser 
y 
. En la imagen podemos observar dos cuencas de atracción claramente diferenciadas. La cuenca correspondiente a está compuesta por todos los puntos correspondientes al semiplano izquierdo, mientras que la cuenca correspondiente a contiene a todas las estimaciones iniciales del semiplano derecho. Se puede concluir que el método de Newton converge siempre a la raíz más próxima y que, a menor distancia de la estimación inicial respecto de la solución, más rápida es la convergencia.
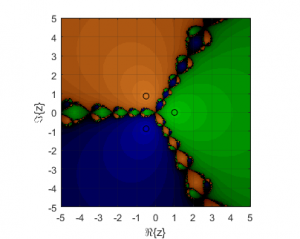
El segundo caso tiene como protagonista a la ecuación no lineal 
, cuyas soluciones son 
. En la imagen observamos un plano dinámico diferente al anterior en varios aspectos. Al tratarse de una ecuación no lineal de tercer grado, hay tres soluciones y, por tanto, tres colores diferentes: naranja para z1 , azul para z2 y verde para z3. Además, hay inmersión de cuencas, de modo que las estimaciones iniciales no convergen a la solución más próxima en todos los casos.
Existen métodos en los cuales no todas las estimaciones iniciales convergen a las soluciones. Sobre estos métodos hay que analizar en profundidad diferentes conceptos dinámicos como son los puntos fijos y sus características, los puntos críticos, y otras representaciones como el plano de parámetros. Se tratan de métodos con peores características de estabilidad, pero que a nivel dinámico poseen una gran riqueza.