Ritmos euclídeos: la música de las matemáticas

Por Neus Garrido.
Esperando en la cola del supermercado, en una estación de trenes e incluso en nuestra casa mientras cocinamos, nos sorprendemos con frecuencia tarareando el ritmo de una canción conocida o incluso moviendo nuestro cuerpo al ritmo de su estribillo. Y dando un paso más, en ocasiones hasta incluso coincidimos con la canción que está recordando el de al lado a pesar de que puede que éste sea un extraño para nosotros.
Tras estas situaciones tan comunes se esconde, entre otras cosas, un razonamiento puramente matemático. Concretamente, la geometría ayuda a explicar las preferencias que solemos tener hacia algunos ritmos musicales o melodías, así como también la existencia de ritmos más “bailables”. No es una casualidad que estas preferencias tengan una inclinación más pronunciada hacia los ritmos que son más homogéneos o uniformes.
A nivel técnico, un ritmo musical es una repetición de un patrón de pulsaciones distribuidos a lo largo de un tramo temporal. Por tanto, se puede interpretar como el problema geométrico de distribuir puntos en un cierto espacio de forma uniforme. En este contexto es donde aparece la relación entre la música y las matemáticas.
Todos conocemos el algoritmo de Euclides para calcular el máximo común divisor de dos números enteros. No obstante, este algoritmo también tiene su aplicación en el universo de la música, ya que tras la aplicación matemática del algoritmo se esconde la construcción de ritmos musicales. Fue Toussaint [1] en 2005 quien aplicó el algoritmo de Euclides a la distribución de acentos musicales en un ritmo musical dando lugar a lo que denominamos ritmos euclídeos. El denominador común de estos ritmos es que sus patrones se distribuyen de la forma más uniformemente posible. Dicha construcción ha dado lugar a los ritmos más utilizados en la historia de la música.
Los ritmos euclídeos se denotan E(n,k), donde n es el número total de pulsos que tiene el ritmo y k es el número de acentos (o pulsos acentuados) que se distribuyen en este ritmo. Mostraremos cómo construir estos ritmos utilizando el algoritmo de Euclides a través de un ejemplo.
Supongamos que queremos distribuir 3 acentos en un total de 8 pulsos. Si aplicamos el algoritmo de Euclides para calcular el máximo común divisor (mcd) de 3 y 8 tendríamos:
8=3·2+2 → 3=2·1+1 → 2=2·1+0
y por tanto mcd(8,3)=mcd(3,2)=mcd(2,1)=1.
Una forma común de representar un ritmo musical es una secuencia binaria, donde cada pulso se considera una unidad de tiempo y denotamos con un 1 aquellos que tienen acento y con un 0 los pulsos no acentuados. En este ejemplo, del total de 8 pulsos, inicialmente tendríamos la secuencia [0 0 0 0 0 1 1 1] cuyos unos distribuiremos de forma uniforme para generar el ritmo euclídeo. Partiendo del estado inicial
0 0 0 0 0 | 1 1 1
el primer paso del algoritmo de Euclides (8=3·2+2) nos indica que debemos formar 3 grupos y nos sobran dos elementos:
0 1 0 1 0 1 | 0 0
El siguiente paso (3=2·1+1) indica que se deben formar dos grupos, sobrando un elemento:
0 1 0 0 1 0 | 0 1
Con el fin del algoritmo, añadiríamos al final de la secuencia el elemento (0 1) sobrante:
[0 1 0 0 1 0 0 1].
Como los ritmos musicales son cíclicos (se repiten de forma sucesiva) podemos aplicar una rotación y comenzar con un acento, de modo que el ritmo euclídeo obtenido es el siguiente:
E(8,3)=[1 0 0 1 0 0 1 0]=[X . . X . . X].
También podemos representarlo geométricamente (Figura 1) considerando las pulsaciones totales del ritmo como puntos de una circunferencia y uniendo los pulsos con acentos dando lugar a figuras geométricas cuya uniformidad puede ser analizada.
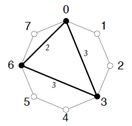
Figura 1. Representación geométrica del ritmo euclídeo E(8,3)
El ritmo euclídeo que acabamos de generar, no es ni más ni menos que el famoso ritmo cubano tresillo, o también llamado en Estados Unidos ritmo Habanera, uno de los ritmos musicales más famosos del mundo.
Música y matemáticas. Dos universos con más puntos en común de los que creemos. Pero ¿dónde empieza la música y dónde terminan las matemáticas?
[1] G.T. Toussaint. The Euclidean Algorithm generates traditional musical rhythms. Proceedings of BRIDGES: Mathematical Connections in Art, Music and Science, 2005, pp. 47—56.
