Computación evolutiva: cómo evitar que el “mono” escriba los programas.
Por Marina de la Cruz
Se comenzará a tratar en este artículo una posible alternativa para que los ordenadores “se programen solos”: la programación automática evolutiva o computación evolutiva. El término “evolutivo” hace referencia al uso de algoritmos genéticos. Estos algoritmos pueden ser considerados como un modelo de cómputo de propósito general. Son en realidad un modelo de búsqueda que incorpora elementos estocásticos aplicable a cualquier dominio.
La computación evolutiva, por tanto, transforma el problema del desarrollo automático de programas en uno de búsqueda compatible con la manera en la que los algoritmos genéticos funcionan.
Es posible que el lector conozca los algoritmos genéticos. Para centrar el contexto de estos párrafos se resumen, a continuación, sus características más relevantes (ver figura 1):
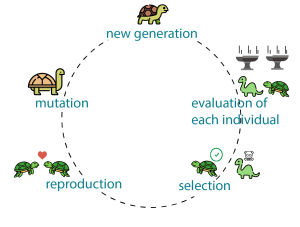
Figura 1: elementos de algoritmos genéticos, adaptada de https://www.generativedesign.org/02-deeper-dive/02-04_genetic-algorithms/02-04-01_what-is-a-genetic-algorithm
Los algoritmos genéticos se inspiran en la selección natural basada en la supervivencia de los individuos más aptos y en la mejora evolutiva de las especies respecto a esa adaptación mediante los mecanismos de reproducción sexual, con compartición de la información genética de los padres, y la variación de esa información gracias a mutaciones.
La figura 1 representa gráficamente estas operaciones:
- La evolución es un ciclo continuo que mejora el conjunto de individuos de la especie actual.
- La competencia por los recursos hace que los menos adaptados no sobrevivan.
- Los mejor adaptados se reproducen generando nuevos individuos cuya información genética es una mezcla de la de sus padres completada con mutaciones provocadas por factores externos.
Para articular un modelo computacional (bio)inspirado en este proceso, es necesario formalizar los siguientes elementos:
- Condiciones de inicio y fin: habitualmente se genera una población inicial esencialmente de individuos cuya información genética se determina al azar. La búsqueda termina cuando la población contiene individuos “suficientemente buenos”.
- Cada individuo de la población se considera un “candidato a solución” del problema por lo que es imprescindible diseñar un mecanismo para representar eficazmente las posibles soluciones al problema como información genética. Inicialmente esta “codificación” de los individuos consistía en representarlos como números binarios. El abaratamiento de los recursos informáticos permite en la actualidad sofisticar enormemente esta codificación como se mostrará en futuras entradas en este mismo blog.
- Hay que diseñar una función que determine, a partir de la codificación anterior, “lo bueno o malo” que es cada individuo. A esta función se la conoce como función de adecuación (o fitness en inglés).
- También es necesario incorporar los mecanismos de reproducción con compartición de información genética y de mutación presentados anteriormente. A estas operaciones se las conoce respectivamente como recombinación (o crossover) y mutación.
- La mutación esencialmente consiste en la elección de unos cuantos bits y su cambio por otro valor.
- La recombinación básicamente consiste en elegir trozos de las cadenas binarias que representan a los padres y combinarlos para formar a los hijos.
- El teorema de los esquemas (Holland92) demuestra que este modelo de computación, que entiende la computación como una búsqueda, “funciona”. Con más precisión, se demuestra que tras una serie de repeticiones del ciclo resumido anteriormente se tiene garantía de que la “bondad” de la población se incrementa siempre, por lo que bastará con determinar el umbral del valor de fitness a partir del cual se considera que la búsqueda es satisfactoria (los individuos encontrados son “suficientemente buenos”).
Este resumen simplificado de los algoritmos genéticos permite vislumbrar la cantidad de parámetros que pueden tener que ajustarse para conseguir las garantías que el teorema de los esquemas asegura: tamaño de la población, proceso concreto de codificación de los individuos y de las operaciones genéticas de recombinación y mutación, tasas de recombinación y mutación, selección de los individuos que se reproducen, forma en la que se reemplaza la generación anterior por la nueva en cada paso del proceso, etc.
¿Cuándo merece la pena utilizar un algoritmo genético en lugar de otra técnica más convencional?
De manera general, las técnicas de búsqueda de propósito general (aplicables a cualquier dominio y, por tanto, ajenas a heurísticas o cualquier otra consideración particular de cada área de aplicación) pueden simplificarse como “aproximaciones de fuerza bruta” que básicamente consisten en recorrer todo el conjunto de posibles elementos entre los que se encuentran los buscados, hasta que los encontremos. A pesar de que el área de la inteligencia artificial propone técnicas optimizadas de búsqueda, es fácil ver que ese procedimiento podría necesitar recorrer todo el conjunto de posibles soluciones. Si las opciones son pocas y este conjunto es pequeño, no merece la pena usar algoritmos genéticos. Es necesario que el espacio de búsqueda sea muy grande para que tenga sentido utilizar estas aproximaciones.
Pero ¿de qué depende el tamaño del espacio de búsqueda? Esencialmente de las características de la codificación. Pongamos un ejemplo muy sencillo: si todas las opciones posibles entre las que están las que nos interesen pueden codificarse realmente como números binarios de 3 bits, está claro que el espacio de búsqueda tendrá 8 elementos. Mucho se debe demorar el proceso que determina si cada elemento es la solución buscada para que el proceso no pueda hacerse mediante aproximaciones convencionales. Imagínese ahora que son necesarios 100 bits para la codificación. El espacio de búsqueda sería de 2^100 opciones, esto es, alrededor de 1,267,650,600,228,229,401,496,703,205,376 elementos. Esta cantidad no invita al optimismo.
Pero ¿cómo puede aplicarse este modelo a la programación automática? Los primeros intentos identificaron la dificultad del proceso. Se descartó la opción directa de tratar los programas como “habitualmente” se trataba al resto de individuos en algoritmos genéticos: codificarlos como una secuencia de bits y aplicar los operadores genéticos de recombinación y mutación que tanto éxito habían tenido en otros dominios.
El tamaño de los individuos posibles implicará un espacio de búsqueda inmanejable. Pero esta no es la principal razón del fracaso. Si se representan los programas como secuencias de bits, la probabilidad de que, tras una operación de recombinación, se generen individuos (programas) inviables, es altísima. Aclaremos este escenario con un ejemplo. Representaremos los programas (individuos) con código C en lugar de su correspondiente secuencia de bits para resaltar la problemática.
Supongamos que los dos programas siguientes forman parte de la población, y que las posiciones de corte para la recombinación son las marcadas en rojo.
int fnc(int x)
{
int aux_return;
aux_return = 0;
for (i=0;i< x;i++)
{
aux_return += i;
}
return aux_return;
}
int fnc(int x)
{
return 2*x;
}
Se obtendrían los dos siguientes programas tras recombinar a estos dos padres, que claramente son incorrectos.
int fnc(int x)
{
int aux_return;
aux_return = 0;
for (i=2*x;
}
int fnc(int x)
{
return 0;i< x;i++)
{
aux_return += i;
}
return aux_return;
}
¿Qué probabilidades de obtener un hijo “con algún sentido” tiene esta codificación? Casi las mismas de que un mono “al teclado” escribiera la función buscada.
Hace unas décadas J.R.Koza (Koza92), considerado el creador de la programación genética, tuvo una idea mejor. La figura 2 muestra su propuesta para representar código como por ejemplo las expresiones doble(6) o 3*4+2.
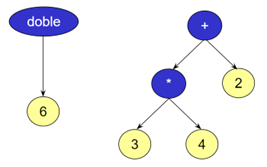
Figura 2. Representación propuesta por J.R. Koza para representar código en programación genética.
Esta representación de programas en forma de árbol, en lugar de secuencias de bits, posibilitó el uso eficiente de aproximaciones evolutivas a la programación automática.
En próximas entradas de este blog se profundizará en la propuesta de Koza y se presentarán otras alternativas.
[Holland92], J.H., Adaptation in Natural and Artificial Systems, 2aed. Massachusets Institute of Tecnology, MIT Press Ed.1992
[Koza92], J.R.Koza (1992) A genetic approach to the truck backer upper problem and the inter-twined spiral problem. In Proceedings of IJCNN International Joint Conference on Neural Networks, volume IV, pages 310-318. IEEE Press, New York
